(11) X-ray diffraction analysis of the crystals showed a diffraction pattern characteristic of struvite (ammonium magnesium phosphate).(10) Each sarcomere position is stored in a three-dimensional (3-D) matrix array from which Fraunhofer light diffraction patterns have been calculated using numerical methods based on Fourier transforms.
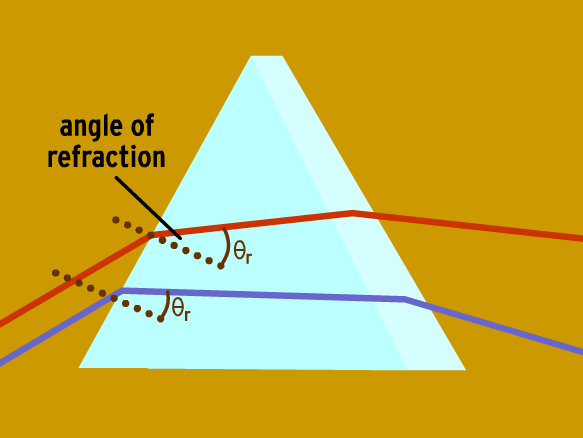
(9) In contrast, the number of substructural lines within the diffraction maxima is large even for microscopically homogeneous fibers.(8) Optical diffraction measurements on electron micrographs of the bend demonstrate that the axostyle tubules slide over one another and that the tubules on the inside of a bend usually contract, sometimes by as much as 25%.(7) The crystals grown at 5 degrees C did not diffract X-rays, while those grown at 18 degrees C and 37 degrees C did.(6) The crystals diffract to at least 2.2 A Bragg spacing and are stable to x-rays.
(5) A laser diffraction technique has been developed for registering small changes in sarcomere length. (4) X-ray diffraction spectrum of 1:8 coprecipitate (COPPT) showed no crystalline structure of AD. (3) The calculation, based on analytical expression derived by Cowley, has been shown previously to give an almost quantitative description of kinematical diffraction from linear chain systems. (2) The electron spectroscopic diffraction (ESD) mode of operation of an energy-filtering electron microscope offers the possibility of being able to avoid the background from inelastic scattering in selected-area electron diffraction patterns. (1) Thin films (OD approximately 0.7) of glucose-embedded membranes, prepared as a control, showed virtually 100% conversion to the M state, and stacks of such thin film specimens gave very similar x-ray diffraction patterns in the bR568 and the M412 state in most experiments. (n.) The deflection and decomposition of light in passing by the edges of opaque bodies or through narrow slits, causing the appearance of parallel bands or fringes of prismatic colors, as by the action of a grating of fine lines or bars. This explains why long wavelengths diffract more. As a consequence, the side-going wave is not so dim. But now, they oscillate much slower, meaning that they don't get so much time mismatch (=phase offset) and don't cancel out. The different emitting points will still be at different distances from the detector. You place the detector on the side as we did before. When you do the same reasoning with a longer wavelength, the result changes. As a consequence, these wave cancel each other so the total wave is dimmer on the side. The emitting points will not be all at the same distance to the detector: the waves they emit will all be mismatched with each other (they have a phase offset). Thus, all the spherical waves will be in phase, so they add up, i.e. If you put a detector in front of the hole, sufficiently far away, it will be more or less at the same distance from all the emitting points of the hole. Back to diffraction: we observe what is going on in front of the hole. Waves in phase add up, whereas waves in anti-phase cancel each other. For example, two waves which oscillate at the same time are said in phase. 
It represents the relative temporal delay between waves of the same wavelength. For that, we need to understand the phase of waves. Now, let's see how the wavelength matters. That's basically where diffraction comes from. However, the sides of the wave are bent, because there are no more points to "complete" the wave. When the wave passes through a hole (see this picture), the center of the wave stays flat thanks to the contribution of central emitting points. The wikipedia article shows nice pictures of those re-emitting points. It says that the wave propagation can be seen as a perpetual absorption at all points everywhere, and these points re-emit the absorbed wave as spherical wave. Let's try a hand-waving explanation.Ī very important theorem to understand how waves propagate is the Huygens-Fresnel principle. You can explain diffraction (and refraction!) from classical wave mechanics you don't need quantum mechanics really.
0 kommentar(er)
